数理・データサイエンス学科※
研究の概要
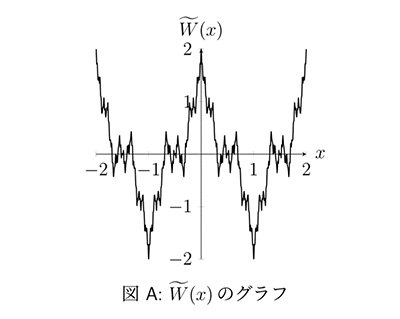
「無限個の関数の和」による関数の表現について研究しています。無限個の和で表される関数には特異な性質を持つものがあります。例えば、どの点においても微分可能でない連続関数の1つにワイエルストラス関数と呼ばれるものがあり、これはcosの無限個の和で構成されます（下図を参照）。
このような「関数の無限和」の理論は信号処理や画像処理などの分野でも応用されています。
近年は石油探索をきっかけに理論の整備が行われているウェーブレットと呼ばれる関数の無限和を研究しており、関数の無限和を通じて関数の持つ連続性や局所性などの特異な性質を調べています。
研究成果の社会での実装、活用シーン
- 自然現象を表現する偏微分方程式の数値解の構成や得られた解の精度などへの応用
- 確率的な振る舞いをする現象のモデル化への応用
- 画像データなどのデータ圧縮への応用
高校生へのメッセージ
近年、生成AIや機械学習、深層学習の研究開発が飛躍的に進展しています。これらのメカニズムやアルゴリズムを理解するためには、高校で学習する微分積分や確率統計の知識のほかに、大学で学ぶ高度な数学の知識が必要になります。純粋数学だけでなく社会に役立つ実用的な数学を一緒に学んでいきましょう。