確率解析―ランダムで微分できない関数についての微積分学
Yuki Hirai
平井 祐紀助教、博士(理学)
確率論、数理ファイナンス
数理・データサイエンス学科

研究の概要
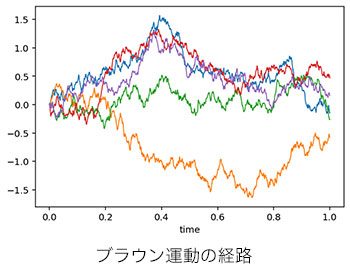
時間経過にともない滑らかに変化する現象を調べるためには、微分積分学や微分方程式といった手法が用いられます。一方、世の中にはランダムなノイズの影響により、非常に複雑で滑らかでない変化をする現象も数多く存在します。その典型例はブラウン運動と呼ばれる微小な粒子の運動で、最も重要な確率過程の一つです。この手の現象と通常の微積分学はあまり相性がよくありませんが、確率積分や確率微分方程式という確率論的な手法を用いると調べることができます。確率過程に関するこれらの解析手法は、確率解析と呼ばれています。
確率解析においては現象の背後にある確率分布が重要ですが、それを正確に推定することは容易ではありません。そのため、確率分布の選択によらない形で確率解析の理論を展開することが、一つの重要な課題となっています。私もそのような観点から確率解析の研究を行っています。
研究成果の社会での実装、活用シーン
数学の応用というと、自然科学や工学などいわゆる「理系」の領域を思い浮かべる方が多いでしょう。私の研究している確率解析は、実は金融市場の分析など経済学の分野にも用いられています。皆さんも株や為替の値動きのグラフをニュース等で見たことがあるかと思います。それらは先ほど説明したブラウン運動のように複雑な動きをするため、その解析には確率解析の手法が有用です。実際に、金融機関では数学の専門知識を持つ人々が高度な数学モデルを金融市場の分析に利用しています。
高校生へのメッセージ
高校生の皆さんの中には、数学に対して「ひたすら複雑な計算を続けるだけの苦行」というようなイメージを持っている人も少なくないのではないでしょうか。もちろんそのような一面もありますが、決してそれだけが数学の全てではありません。数学を学ぶ上では、仮定をもとに筋道を立ててきちんと考えるという力がとても大切になります。数字があまり好きでなくても、考えるのが好きな人はぜひ一生懸命数学を勉強してみてください。実際にやってみると、数学とはとても楽しいものです。